python3-scipy卷积定理和频域高斯模糊
发布时间:2021-08-25 23:01:53编辑:run阅读(9512)
Scipy卷积定理和频域高斯模糊.
卷积定理的应用,卷积定理是指在图像域中的卷积等价于频域中的简单乘法。
卷积定理:f(x, y) * h(x, y) <==> F(u, v)H(u, v) 空域卷积=频域乘法
频域滤波的基本步骤。将原始图像F和核(掩模,退化或增强函数)作为输入。首先两个输入项都需要用DFT转换成频域,然后应用卷积(根据卷积定理,一个元素的乘法)。将卷积后的图像输出到频域,在频域上应用IDFT得到重建后的图像(对原始图像进行一定的退化或增强)。
带有numpy fft的频域高斯模糊滤波器
from skimage.io import imread
import scipy.fftpack as fp
import matplotlib.pylab as pylab
import numpy as np
from scipy import signal
# 指定默认字体
pylab.rcParams['font.sans-serif'] = ['KaiTi']
# 解决保存图像是负号'-'显示为方块的问题
pylab.rcParams['axes.unicode_minus'] = False
pylab.figure(figsize=(20, 15))
pylab.gray()
im = np.mean(imread(r'D:\image_processing\image_two\1dd.jpg'), axis=2)
gauss_kernel = np.outer(signal.gaussian(im.shape[0], 5), signal.gaussian(im.shape[1], 5))
freq = fp.fft2(im)
assert(freq.shape == gauss_kernel.shape)
freq_kernel = fp.fft2(fp.ifftshift(gauss_kernel))
convolved = freq * freq_kernel
im1 = fp.ifft2(convolved).real
pylab.subplot(2, 3, 1)
pylab.imshow(im)
pylab.title('原始图像',size=25)
pylab.axis('off')
pylab.subplot(2, 3, 2)
pylab.imshow(gauss_kernel)
pylab.title('高斯核',size=25)
pylab.axis('off')
pylab.subplot(2, 3, 3)
pylab.imshow(im1)
pylab.title('输出图像',size=25)
pylab.axis('off')
pylab.subplot(2, 3, 4)
pylab.imshow((20*np.log10(0.1+fp.fftshift(freq))).astype(int))
pylab.title('原始图像频谱',size=25)
pylab.axis('off')
pylab.subplot(2, 3, 5)
pylab.imshow((20*np.log10(0.1+fp.fftshift(freq_kernel))).astype(int))
pylab.title('高斯核频谱',size=25)
pylab.axis('off')
pylab.subplot(2, 3, 6)
pylab.imshow((20*np.log10(0.1+fp.fftshift(convolved))).astype(int))
pylab.title('输出图像频谱',size=25)
pylab.axis('off')
pylab.subplots_adjust(wspace=0.2, hspace=0)
pylab.show()
可以看到其中包括在空域上的原始图像,高斯核,卷积后的图像,以及在频域上的原始频谱,高斯核频谱和输出图像频谱。
二维高斯LPF核频谱,如何用对数变换在二维图中绘制高斯核的频谱:
from skimage.io import imread import scipy.fftpack as fp from skimage.color import rgb2gray import matplotlib.pylab as pylab import numpy as np from scipy import signal im = rgb2gray(imread(r'D:\image_processing\image_two\1dd.jpg')) gauss_kernel = np.outer(signal.gaussian(im.shape[0], 1), signal.gaussian(im.shape[1], 1)) freq = fp.fft2(im) freq_kernel = fp.fft2(fp.ifftshift(gauss_kernel)) pylab.imshow((20*np.log10(0.01+fp.fftshift(freq_kernel))).real.astype(int), cmap='coolwarm') pylab.colorbar() pylab.show()
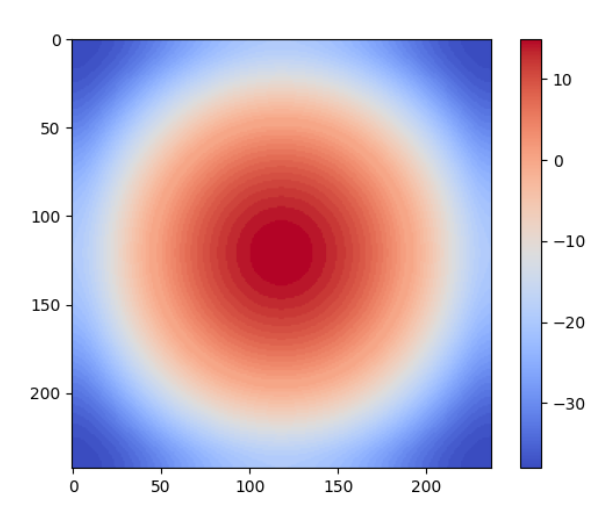
可以看到,图中有一个颜色条,因为高斯核是一种低通滤波器,它的频谱对于中心的频谱有较高的值(允许更多的低频值),并且随着值从中心向高频值的移动而逐渐减小。
三维高斯核频谱。
import numpy as np
import matplotlib.pyplot as plt
import math
# 指定默认字体
pylab.rcParams['font.sans-serif'] = ['KaiTi']
# 解决保存图像是负号'-'显示为方块的问题
pylab.rcParams['axes.unicode_minus'] = False
x, y = np.mgrid[-2:2:200j, -2:2:200j]
z=(1/2*math.pi*3**2)*np.exp(-(x**2+y**2)/2*3**2)
ax = plt.subplot(111, projection='3d')
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow', alpha=0.1)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('三维高斯核',size=25)
plt.show()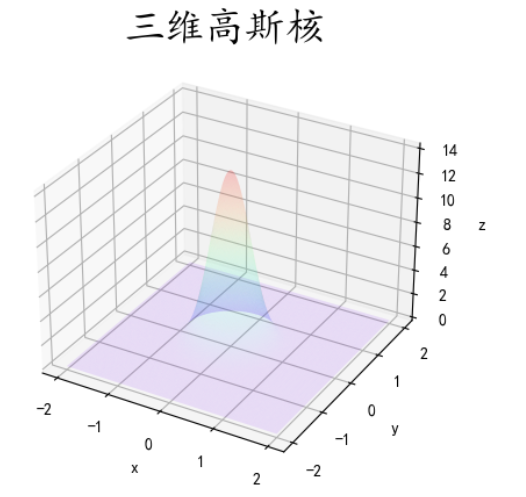
- openvpn linux客户端使用
52073
- H3C基本命令大全
51949
- openvpn windows客户端使用
42172
- H3C IRF原理及 配置
39014
- Python exit()函数
33516
- openvpn mac客户端使用
30472
- python全系列官方中文文档
29102
- python 获取网卡实时流量
24137
- 1.常用turtle功能函数
24039
- python 获取Linux和Windows硬件信息
22384
- LangChain1.0-Agent-部署/上线(开发人员必备)
156°
- LangChain1.0-Agent-Spider实战(爬虫函数替代API接口)
183°
- LangChain1.0-Agent(进阶)本地模型+Playwright实现网页自动化操作
190°
- LangChain1.0-Agent记忆管理
171°
- LangChain1.0-Agent接入自定义工具与React循环
189°
- LangChain1.0-Agent开发流程
178°
- LangChain1.0调用vllm本地部署qwen模型
210°
- LangChain-1.0入门实践-搭建流式响应的多轮问答机器人
212°
- LangChain-1.0入门实战-1
217°
- LangChain-1.0教程-(介绍,模型接入)
220°
- 姓名:Run
- 职业:谜
- 邮箱:383697894@qq.com
- 定位:上海 · 松江
