最短路径算法—Floyd(弗洛伊德)算法

发布时间：2019-07-22 17:40:19编辑：auto阅读（2554）

    December 19, 2015 10:56 PM
    Floyd算法是解决任意两点间的最短路径的一种算法，可以正确处理带权有向图或负权的最短路径问题
    解决此问题有两种方法：
    其一是分别以图中每个顶点为源点共调用n次算法；
    其二是采用Floyd算法。
    两种算法的时间复杂度均为O(n3)，但后者形式上比较简单。

    Floyd算法的基本思想：
    1. 利用二维数组dist[i][j]记录当前vi到vj的最短路径长度，数组dist的初值等于图的带权邻接矩阵;
    2. 集合S记录当前允许的中间顶点，初值S=Φ;
    3. 依次向S中加入v0 ,v1… vn-1，每加入一个顶点，对dist[i][j]进行一次修正：设S={v0 ,v1… vk-1}，加入vk，则dist(k)[i][j] = min{ dist(k-1)[i][j]，dist(k-1)[i][k]+dist(k-1)[k][j]}。dist(k)[i][j]的含义：允许中间顶点的序号最大为k时从vi到vj的最短路径长度。
    dist(n-1)[i][j]就是vi到vj的最短路径长度。
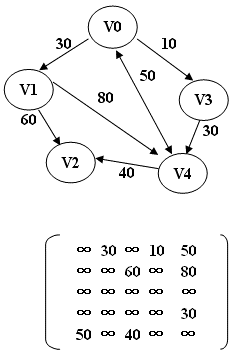
    这里写图片描述

    最短距离有三种情况：
    １、两点的直达距离最短。
    ２、两点间只通过一个中间点而距离最短。
    ３、两点间用通过两各以上的顶点而距离最短。
    对于第一种情况：
    在初始化的时候就已经找出来了且以后也不会更改到。
    对于第二种情况：
    弗洛伊德算法的基本操作就是对于每一对顶点，遍历所有其它顶点，看看可否通过这一个顶点让这对顶点距离更短
    对于第三种情况：
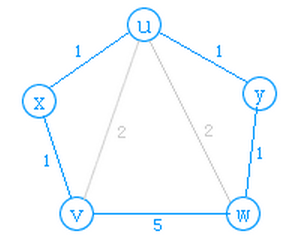
    如下图的五边形，可先找一点（比如x，使=2），就变成了四边形问题，再找一点（比如y,使=2），可变成三角形问题了（v,u,w），也就变成第二种情况了，由此对于n边形也可以一步步转化成四边形三角形问题。（这里面不用担心哪个点要先找哪个点要后找，因为找了任一个点都可以使其变成（n－1）边形的问题）。
    这里写图片描述

    #Floyd.py
#王渊
#2015.12.17
#Email:wyxidian@gmail.com
from pylab import *

INFINITY = 65535                        #代表无穷大
D = array([[0,10,INFINITY,INFINITY,INFINITY,11,INFINITY,INFINITY,INFINITY],#邻接矩阵
        [10,0,18,INFINITY,INFINITY,INFINITY,16,INFINITY,12],
        [INFINITY,18,0,22,INFINITY,INFINITY,INFINITY,INFINITY,8],
        [INFINITY,INFINITY,22,0,20,INFINITY,INFINITY,16,21],
        [INFINITY,INFINITY,INFINITY,20,0,26,INFINITY,7,INFINITY],
        [11,INFINITY,INFINITY,INFINITY,26,0,17,INFINITY,INFINITY],
        [INFINITY,16,INFINITY,24,INFINITY,17,0,19,INFINITY],
        [INFINITY,INFINITY,INFINITY,16,7,INFINITY,19,0,INFINITY],
        [INFINITY,12,8,21,INFINITY,INFINITY,INFINITY,INFINITY,0]])
lengthD = len(D)                    #邻接矩阵大小
p = list(range(lengthD))
P = []
for i in range(lengthD):
    P.append(p)
P = array(P)

for i in range(lengthD):
    for j in range(lengthD):
        for k in range(lengthD):
            if(D[i,j] > D[i,k]+D[j,k]):         #两个顶点直接较小的间接路径替换较大的直接路径
                P[i,j] = P[j,k]                 #记录新路径的前驱
print(P)
print(D)

关键字：

上一篇： python脚本生成html

下一篇： windows/linux环境pytho