1、傅里叶变换
傅里叶变换是信号领域沟通时域和频域的桥梁,在频域里可以更方便的进行一些分析。傅里叶主要针对的是平稳信号的频率特性分析,简单说就是具有一定周期性的信号,因为傅里叶变换采取的是有限取样的方式,所以对于取样长度和取样对象有着一定的要求。
2、基于Python的频谱分析
将时域信号通过FFT转换为频域信号之后,将其各个频率分量的幅值绘制成图,可以很直观地观察信号的频谱。
具体分析见代码注释。
import numpy as np#导入一个数据处理模块 import pylab as pl#导入一个绘图模块,matplotlib下的模块 sampling_rate = 8000#采样频率为8000Hz fft_size = 512 #FFT处理的取样长度 t = np.arange(0, 1.0, 1.0/sampling_rate)#np.arange(起点,终点,间隔)产生1s长的取样时间 x = np.sin(2*np.pi*156.25*t) + 2*np.sin(2*np.pi*234.375*t)#两个正弦波叠加,156.25HZ和234.375HZ # N点FFT进行精确频谱分析的要求是N个取样点包含整数个取样对象的波形。因此N点FFT能够完美计算频谱对取样对象的要求是n*Fs/N(n*采样频率/FFT长度), # 因此对8KHZ和512点而言,完美采样对象的周期最小要求是8000/512=15.625HZ,所以156.25的n为10,234.375的n为15。 xs = x[:fft_size]# 从波形数据中取样fft_size个点进行运算 xf = np.fft.rfft(xs)/fft_size# 利用np.fft.rfft()进行FFT计算,rfft()是为了更方便对实数信号进行变换,由公式可知/fft_size为了正确显示波形能量 # rfft函数的返回值是N/2+1个复数,分别表示从0(Hz)到sampling_rate/2(Hz)的分。 #于是可以通过下面的np.linspace计算出返回值中每个下标对应的真正的频率: freqs = np.linspace(0, sampling_rate/2, fft_size/2+1) # np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None) #在指定的间隔内返回均匀间隔的数字 xfp = 20*np.log10(np.clip(np.abs(xf), 1e-20, 1e100)) #最后我们计算每个频率分量的幅值,并通过 20*np.log10()将其转换为以db单位的值。为了防止0幅值的成分造成log10无法计算,我们调用np.clip对xf的幅值进行上下限处理 #绘图显示结果 pl.figure(figsize=(8,4)) pl.subplot(211) pl.plot(t[:fft_size], xs) pl.xlabel(u"Time(S)") pl.title(u"156.25Hz and 234.375Hz WaveForm And Freq") pl.subplot(212) pl.plot(freqs, xfp) pl.xlabel(u"Freq(Hz)") pl.subplots_adjust(hspace=0.4) pl.show()
3、绘图结果显示
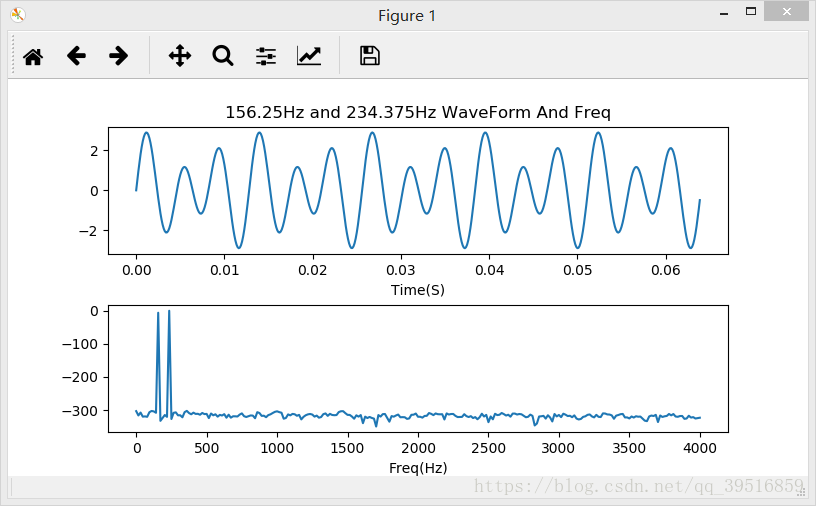
如果你放大其频谱中的两个峰值的部分的话,可以看到其值分别为:
>>>xfp[10] -6.0205999132796251 >>>xfp[15] -9.6432746655328714e-16
即156.25Hz的成分为-6dB, 而234.375Hz的成分为0dB,与波形的计算公式中的各个分量的能量(振幅值/2)符合。
---------------------
作者:赵至柔
来源:CSDN
原文:https://blog.csdn.net/qq_39516859/article/details/79794549
版权声明:本文为博主原创文章,转载请附上博文链接!
