交变应力参数表

跳转到我的博客

交变应力图

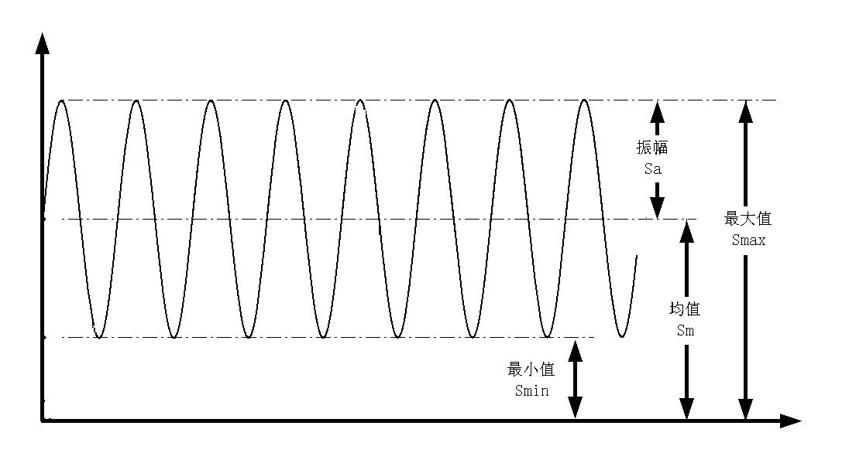
交变应力参数说明

最大应力

\[{{S}_{\max }}\]

最小应力

\[{{S}_{\min }}\]

平均应力

\[{{S}_{\text{m}}}=\frac{1}{2}\left( {{S}_{\max }}+{{S}_{\min }} \right)\]

应力比（应力特征）

\[R=\frac{{{S}_{\min }}}{{{S}_{\max }}}\]

应力振幅

\[{{S}_{a}}=\frac{1}{2}\left( {{S}_{\max }}-{{S}_{\min }} \right)={{S}_{\text{m}}}\left( \frac{1-R}{1+R} \right)\]

上述五个参数之间的关系

变量	定义
\(S_{max}\)	\(S_{max} = S_m +S_a\)
\(S_{min}\)	\(S_{min} = S_m - S_a\)
\(S_m\)	\(S_m = \frac{1}{2}(S_{max}+S_{min})\)
\(S_{a}\)	\(S_{a} = \frac{1}{2}(S_{max}-S_{min})\)
\(R\)	\(R=\frac{S_{min}}{S_{max}}\)

等寿命曲线

\[{{S}_{\max }}=\frac{2{{S}_{m}}}{1+R}\]
\[{{S}_{\min }}=\frac{2{{S}_{m}}}{1+\frac{1}{R}}\]

部分计算

应力比	平均应力	最大应力	最小应力	应力振幅
\(R\)	\({{S}_{m}}\)	\({{S}_{\max }}\)	\({{S}_{\min }}\)	\({{S}_{a}}\)
-1	0	\({{S}_{\max }}\)	-\({{S}_{\max }}\)	\({{S}_{\max }}\)	对称循环应力
0	\({{S}_{m}}\)	2\({{S}_{m}}\)	0	\({{S}_{m}}\)
0.1	\({{S}_{m}}\)	1.81818\({{S}_{m}}\)	0.18181\({{S}_{m}}\)	0.81818\({{S}_{m}}\)
0.2	\({{S}_{m}}\)	1.66667\({{S}_{m}}\)	0.33333\({{S}_{m}}\)	0.66666\({{S}_{m}}\)
0.3	\({{S}_{m}}\)	1.53846\({{S}_{m}}\)	0.46154\({{S}_{m}}\)	0.53846\({{S}_{m}}\)
0.4	\({{S}_{m}}\)	1.42857\({{S}_{m}}\)	0.57143\({{S}_{m}}\)	0.42857\({{S}_{m}}\)
0.5	\({{S}_{m}}\)	1.33333\({{S}_{m}}\)	0.66667\({{S}_{m}}\)	0.33333\({{S}_{m}}\)
1	\({{S}_{m}}\)	\({{S}_{m}}\)	\({{S}_{m}}\)	0	静力

python函数设计

# 5各变量，其中已知两个，其它的都可以知道。
def changestress(R, Sa):
    if R==1 or Sa==0:
        return "Static Load"
    else:
        Smax = 2*Sa/(1-R)
        Smin = 2*Sa*R/(1-R)
        Sm = (1+R)*Sa/(1-R)
        return {'Smax':Smax, 'Smin':Smin, 'Sm':Sm}

Python代码

from sympy import *

Sm = symbols('Sm')
Smax = []
Smin = []
Sa = []

Range = [0.1, 0.2, 0.3, 0.4, 0.5]
for R in Range:
    Smax.append(2*Sm/(1+R))
    Smin.append(2*Sm/(1+1/R))
    Sa.append(Sm*((1-R)/(1+R)))