如何用UIKit做一个转轮(3)
发布时间:2019-08-28 09:10:14编辑:auto阅读(2311)
A Digression Into Trigonometry(三角函数的介绍)
在学校里我们都学过如何用度表示角度,并且我们都知道一个圆有360度。但是科学家、工程师以及程序语言的设计者使用一种叫做弧度的单位。
你也许会记得上面drawWheel的代码在section#2处使用了表达式2*M_PI来计算圆的大小并分割为几个扇区。这是因为360度精确的等于2*M_PI。使用这个公式,我们可以推算出1弧度等于180/PI,并且1度等于P1/180弧度。
这就给了我们度与弧度的转换公式!但是让我们来形象化的显示它们之间的关联。
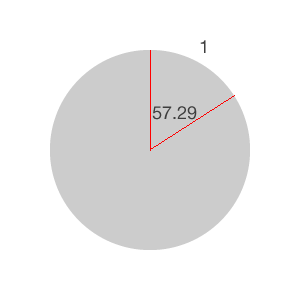
上面这张图片显示了一弧度的“长度”,大约等于57.29度。我们说大约是因为PI是一个无限小数。
还有一种解释方法。如果你根据上面图片中红线对圆的周长进行分割并你把它画直为一条直线,这条线会跟圆的半径有相同的长度。
换句话说,如果按一个角度划分的弧的长度等于半径,那么这个角度的大小为1弧度。非常酷!不是么?
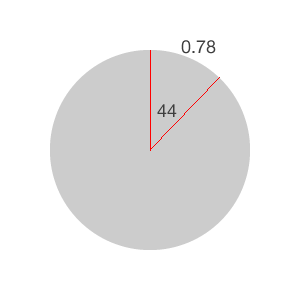
另一个重要的情况是,除了半径的长度,一整个圆还有2*PI个弧度。当你把旋转应用到转轮上时会非常有用。你会把圆分割成8个相等的块,所以每个块大约0.78弧度,即2*PI/8。
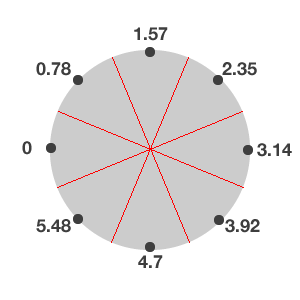
你会从左侧触摸这个圆,按顺时针方向转,所以0弧度应该在左侧。下面的图片显示了你这个方案中八个扇区的角度和弧度的值。
黑色的小点代表每个扇区在弧度上的中间点。正如你从上边的drawWheel方法中看到的,为了让每一个扇区旋转,你要创建一个仿射转换affine transform(of type rotation)并且把它设置为容器container的一个property。像这样:
CGAffineTransform t = CGAffineTransformRotate(container.transform, newValueInRadians);
container.transform = t;
|
不幸的是,参数newValueInRadians不是你想要转动到的点,它是要从当前值增加\减去的弧度的值。你不能说“旋转到x弧度”。你必须计算当前值和x的不同,然后加上\减去那部分。
例如,你可以创建一个timer来定期的旋转轮子。第一步让我们在SMRotaryWheel.h中initWithFrame方法定义的下面添加方法的定义:
-(void)rotate;
|
然后,在SMRotaryWheel.m中的initWithFrame 方法中的section#3下边加上一下代码:
// 4 - Timer for rotating wheel
[NSTimer scheduledTimerWithTimeInterval:2.0 target:self
selector:@selector(rotate)
userInfo:nil
repeats:YES];
|
最后,在SMRotaryWheel.m的最后(在@end的前边)增加rotate方法:
- (void) rotate {
CGAffineTransform t = CGAffineTransformRotate(container.transform, -0.78);
container.transform = t;
}
|
这里,我们选择-0.78是因为它是旋转一个扇区所要给与的一个必要弧度值,如上所述,我们有8个扇区。
编译并运行。你会看到轮子没两秒完成一次旋转。这或多或少跟你最后要完成的应用差不多,尽管你还得用到用户的触摸。这就把我们带到了最棘手的部分。
Adding Rotation(添加旋转)
如果你曾经通过代码的方式实现你需要输入的文字,拿它听起来太容易了:
l 当用户轻碰屏幕,存储弧度的“当前值”
l 每当用户用手指拖拽,计算新的弧度值并用仿射转换进行设置
l 当用户的手指离开屏幕,计算当前选择的扇区并用旋转校准轮子的中心
但是正如常言所说,魔鬼都在细节当中。
为了计算轮子所要旋转的角度,你需要把笛卡尔坐标转换为极点坐标。这意味着什么?
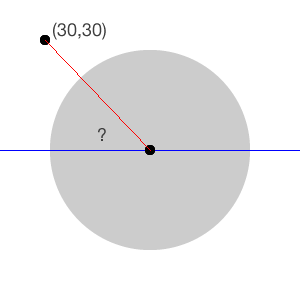
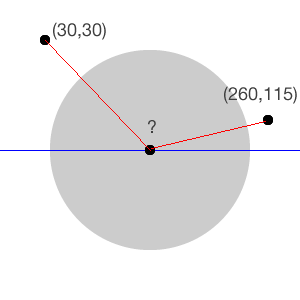
当你检测组件上的一个轻碰时,你可以根据一个“参考点”获得它的笛卡尔坐标系中的x和y值,这个参考点往往是组件的左上角。在这个方案中,你处在一个“圆圈的”世界,在这个世界里,极点pole是这个容器container的中心。例如,在下面的图片中我们说用户点在轮子的(30,30)这个点上。
用户触碰的点和x轴(蓝色的线)之间的夹角是多少呢?你需要知道这个值才能计算用户的手指在轮子上拖拽所划过的角度。这就是要加载到容器container上旋转的角度。
你要对这个计算方法抓狂和努力了。计算上面说的角度要用到反三角函数,三角函数的反函数。你猜猜看,这个函数返回一个弧度值,这正好就是你所需要的!
但是还有一点难处理的小细节,就是反三角函数的输入输出都是PI。如果你记得,我们上面提到过,你的角度范围是从0到2PI,这不是不能处理,但是你得在以后的计算中注意此事。否则,屏幕上显示的效果会非常的怪异。
理论讲的够多了,让我们来看看代码!在SMRotaryWheel.h中,添加一个新的属性property:
@property CGAffineTransform startTransform;
|
当用户触摸组件时会用来存储转换差。为了在用户触摸组件时保存角度,我们在SMRotaryWheel.m的顶部添加一个float类型的静态变量,就写在@implementation的上面:
static float deltaAngle;
|
你也要早先的synthesize这个startTransform属性:
@synthesize startTransform;
|
现在,我们要检测用户触摸了。当用户轻拍一个组件的实例时,轻拍事件会被beginTrackingWithTouc:touch withEvent:event方法处理。在SMRotaryWheel.m中rotate方法的下边重写这个方法:
注意:如果你选择的是扩展UIView而不是UIControl,这个要重写的方法是touchesBegan:touches withEven:event。
- (BOOL)beginTrackingWithTouch:(UITouch *)touch withEvent:(UIEvent *)event {
// 1 - Get touch position
CGPoint touchPoint = [touch locationInView:self];
// 2 - Calculate distance from center
float dx = touchPoint.x - container.center.x;
float dy = touchPoint.y - container.center.y;
// 3 - Calculate arctangent value
deltaAngle = atan2(dy,dx); // 4 - Save current transform
startTransform = container.transform;
return YES;
}
|
第一步你要先找到转轮上触摸点的笛卡尔坐标,然后计算触摸点和容器container中心点的差。最后,你要得到反三角函数值并存储当前的转换差,这样每当用户拖拽轮子时就有一个初始的参考点。
一会你就会看到,你要从这个方法返回YES因为用户拖拽必须被相应。现在在用户触摸开始时你已经保存了这个角度,下一步是根据用户的拖拽计算弧度。
举个例子,我们假设用户触碰组件的点为(50,50),并拖拽到点(260,115)。
你要计算最后这个点的弧度值并从当用户触碰组件时保存的三角形中减去这个值,这个结果就是要传给仿射变换的弧度值。这些会在组件抛出的每一次拖拽事件中实现,在beginTrackingWithTouch方法下边增加这个重写的函数continueTrackingWithTouch:
注意:如果你继承自UIView,需重写的方法是 touchesMoved:withEvent:
- (BOOL)continueTrackingWithTouch:(UITouch*)touch withEvent:(UIEvent*)event
{
CGPoint pt = [touch locationInView:self];
float dx = pt.x - container.center.x;
float dy = pt.y - container.center.y;
float ang = atan2(dy,dx); float angleDifference = deltaAngle - ang;
container.transform = CGAffineTransformRotate(startTransform, -angleDifference);
return YES;
}
|
你会注意到,弧度的计算非常类似与beginTrackingWithTouch方法中所写代码。你也会注意到参数-angleDifference,它会补偿负象限的值。
最后,不要忘记在initWithFrame方法中section#4出的提示:这样轮子才不会自动旋转。
现在编译并运行,看见了吗?你已经做到这一步了!你现在已经有了一个能工作的转轮的原型,它工作的很好!
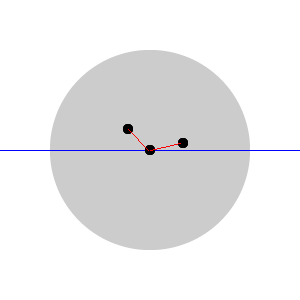
尽管还有一些古怪。例如,如果用户轻拍在靠近轮子中心的一个点上,程序会继续,大事旋转会变得有些“跳跃”。这是因为角度的描绘非常的“混乱”,就像下面这张图。
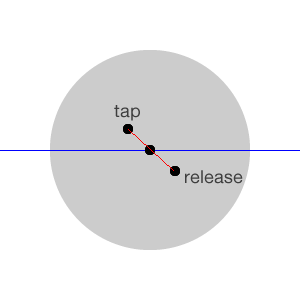
如果用手指划过轮子的中点,“跳跃”会更严重,看下图。
你可以用当前实现的效果验证这个问题。然而代码是工作的,结果也是正确的。
要解决这个问题,就要借助真实的轮子用到的解决方案,就像一个较旧但完好的旋转式拨号盘,拨号盘如果是从较远的地方转到中心点,那么会很难用!你的任务就是忽略太靠近轮子中心的触摸,通过阻止这样的触碰发生时而响应的事件。
要达到这个效果,没有必要使用反三角函数,勾股定理就足够了。但是你需要一个帮助函数,calculateDistanceFromCenter,把它添加在SMRotaryWheel.m的顶部,在drawWheel定义的下边即可:
@interface SMRotaryWheel()
...
- (float) calculateDistanceFromCenter:(CGPoint)point;
|
在continueTrackingWithTouch方法下面进行实现:
- (float) calculateDistanceFromCenter:(CGPoint)point {
CGPoint center = CGPointMake(self.bounds.size.width/2, self.bounds.size.height/2);
float dx = point.x - center.x;
float dy = point.y - center.y;
return sqrt(dx*dx + dy*dy); }
|
这仅仅计算出了这个触碰点与中心点的距离。现在在beginTrackingWithTouch:withEvent:方法的section#1处添加代码:
// 1.1 - Get the distance from the center
float dist = [self calculateDistanceFromCenter:touchPoint];
// 1.2 - Filter out touches too close to the center
if (dist < 40 || dist > 100)
{
// forcing a tap to be on the ferrule
NSLog(@"ignoring tap (%f,%f)", touchPoint.x, touchPoint.y);
return NO;
}
}
|
这样,当触碰点与中心点太近的话,这个触摸会被简单的忽略因为你返回了NO,表明组件不会处理此次触摸事件。
注意:如果你选择的继承UIView,你得在touchesMoved:withEvent方法中实现。
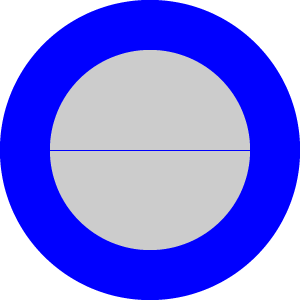
你可以根据你轮子的大小自定义可触摸区域的大小,通过调整section#1.2第一行两个值(40 和 100),类似下边这张图片展示的(蓝色区域):
你也许想在continueTrackingWithTouch:withEvent方法中进行同样的检查。
下面是比较困难的一部分。你要实现的是一个“come-to-rest”的效果,就是当用户的手指离开屏幕的时候,轮子会停在当前扇区的中间点。
上一篇: 精通MVC3摘译(4)-使用Area
下一篇: Unity3D脚印3——Transfor
- openvpn linux客户端使用
52200
- H3C基本命令大全
52106
- openvpn windows客户端使用
42274
- H3C IRF原理及 配置
39142
- Python exit()函数
33644
- openvpn mac客户端使用
30602
- python全系列官方中文文档
29281
- python 获取网卡实时流量
24260
- 1.常用turtle功能函数
24150
- python 获取Linux和Windows硬件信息
22519
- LangChain 1.0-Agent中间件-实现闭环(批准-编辑-拒绝动作)
77°
- LangChain 1.0-Agent中间件-汇总消息
83°
- LangChain 1.0-Agent中间件-删除消息
88°
- LangChain 1.0-Agent中间件-消息压缩
80°
- LangChain 1.0-Agent中间件-多模型动态选择
153°
- LangChain1.0-Agent-部署/上线(开发人员必备)
315°
- LangChain1.0-Agent-Spider实战(爬虫函数替代API接口)
359°
- LangChain1.0-Agent(进阶)本地模型+Playwright实现网页自动化操作
355°
- LangChain1.0-Agent记忆管理
334°
- LangChain1.0-Agent接入自定义工具与React循环
373°
- 姓名:Run
- 职业:谜
- 邮箱:383697894@qq.com
- 定位:上海 · 松江